1926年5月華厳宗大本山東大寺の僧侶たちが開いた夜間の学校が出発点、ひとりひとりの生徒の個性を大切に、生徒の自主性を重んずる教育が伝統の東大寺学園中学校、2012年度「算数」の入試問題にいざ挑戦。
(問題提供:英俊社)
東大寺学園中学校 2012年度「算数」入試問題より
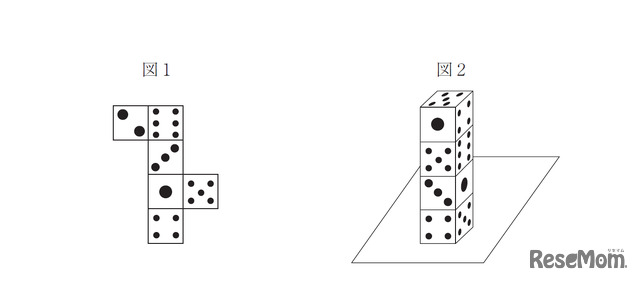
問題:図1の展開図を組み立てて作ったサイコロが4個あります。この4個のサイコロを図2のように木の机の上に積みました。「隠れている(どの方向からも見えない)面」の目の数の和を求めなさい。
解説・解き方
図2のようにサイコロを積むとき、隠れている面は、下の3個のサイコロでは、向かい合う面が1組ずつ、一番上のサイコロでは、5と向かいあう面になる。
図1より、サイコロの向かい合う面の数の和は7なので、一番上のサイコロの隠れている面の数は、7-5=2
残り3個のサイコロの隠れている面の数の和は、7×3=21
よって、求める数の和は、21 +2 =23
解答はこちらから。